
The first of these is instrumental error, the inability of the instrument to correctly measure the flow field. Such errors can result if the current meter rotors are not properly designed, so that wave velocities cause the rotors to spin too quickly. Propellor velocity sensors used on the Vector Measuring Current Meters (VMCMs)(see Reference 1) were designed to eliminate these errors, with the rotors only responding to that component which was parallel with the axis of rotation.
Even with a current meter which measures the velocity perfectly, there are at least two more potential problems with the measurements in the presence of surface waves. The first of these is aliasing. In most conventional deployments the velocities measured by the current meter must be averaged over 1-2 minutes time, while the surface waves have periods of 5-15 seconds. While the averaged current does reflect the true average, variations in that current may be due to the sampling period not being perfectly in phase with the surface waves. High sampling rates can overcome this problem, but may not be an option for very long deployments.

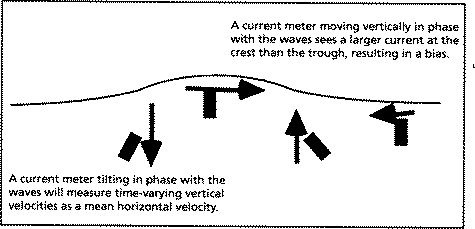
Figure 1
Another source of error is the motion of current meters in phase with the surface gravity waves. Surface waves have a larger velocity along their direction of propagation at the crest of the wave than they do in the reverse direction at the trough of the wave. As a result, particles at a fixed depth drift in the same direction as the waves. Current meters on a mooring will move up and down in phase with the surface waves. Therefore, they will see larger velocities at the crest of the wave than at the trough, resulting in a "wave bias velocity" (a difference between the average current measured around the averaged depth, and the averaged current measured at that depth). At the surface the wave bias will be equivalent to the Stokes drift, but at depth it will be larger. This is because current meters at all depths move up and down with the surface, making excursions much larger than those associated with the gravity waves which die off exponentially on scales of 10-25 meters. A further complication is that current meters may tilt in phase with the waves, so that the "horizontal" current may actually contain components of vertical velocities as well. These problems are illustrated in Figure 1.
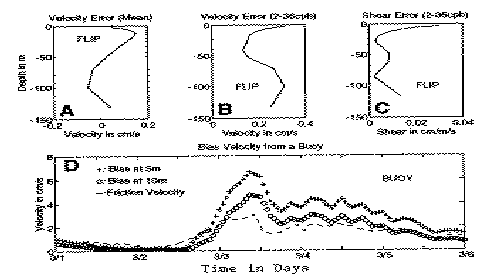
Figure 2
Are these errors small or large? Recent work (see Reference 2) considered the question for a string of 14 VMCMs hung from a boom on the Floating Instrument Platform (FLIP). The string was treated as a multiple pendulum forced by motions of the fulcrum and by the drag and pressure forces generated by the waves. The errors are shown in Figure 2A-C for a time period during which the waves were high. The errors in the mean velocity and shear are much smaller than back of the envelope calculations based on a single wave frequency which are of order 1-2 cm/s. The reason is that the string only responds at a few resonant frequencies, and because wave energy is spread out over a spectrum there is relatively little energy at the right frequencies to excite motions. This will not necessarily be true for shorter strings, however.
For a buoy, however, mean errors are potentially quite a bit larger. Figure 2D shows a time series of computed wave bias from a directional buoy deployed off Bermuda in March of 1994. Bias velocities at 5 and 10 meters are shown, and are demonstrated to be of similar magnitude to the friction velocity. Thus buoy measurements have larger inherent errors in the shear than current meters suspended from a relatively stable platform.
[2] Gnanadesikan, A., 1994, Langmuir circulations in oceanic surface layers, Doctoral Dissertation, MIT/WHOI Joint Program in Oceanography and Oceanographic Engineering, WHOI Tech. Report, 94-23, 354 pp.
 Return to UOP Homepage
Return to UOP Homepage